I spent the last few years studying Bayesian statistics in my spare time. Most recently, I completed Richard McElreath’s Statistical Rethinking - including his 2017 lecture series and problem sets. It is rightfully one of the most popular entry level texts in bayesian statistics. I could not recommend it more highly.

While I’ve gained a lot from doing problem sets and discussing course material with other people, nothing beats testing your knowledge and challenging imposter syndrome by attempting a modelling problem on your own.

So I decided to apply what I’ve learned so far on the Kaggle dataset: House Prices: Advanced Regression Techniques. The goal is to practise what I’ve learned in my self study journey and hopefully demonstrate some of the best practices advocated by those in the applied statistics community. This writeup was completed in R and Python (you’ll get to choose below) and Stan* for modelling.

*Stan is a probabilistic programming language that can flexibly estimate a wide range of probabilistic and bayesian models. It uses state of the art algorithms such as Hamiltonian Monte Carlo (HMC) which allows efficient sampling of models in high dimensions without the need for conjugate priors. Stan is used across academia and industry and notably in facebook’s open source forecasting tool, prophet.

Thinking about workflow

A recurring theme in applied statistics is the importance of workflow. This topic wasn’t really covered explicitly in my econometrics/stats classes which put more emphasis on tools and derivations for predictive or causal inference. At best, components of workflow were explored in some research seminars.

A good workflow supports quality model building. It forces us to think critically about decision making in data analysis which helps us evaluate our assumptions and identify errors. That isn’t to say there is a gold standard of how all data analysis should be conducted. Rather, following a robust methodology guides modelling decisions and helps diagnose problems. This becomes more important when adding complexity into models where it is harder to pinpoint where problems lie.

Developments around workflow are a current topic of research. The most recent paper came out on November 2nd titled Bayesian Workflow which has many contributions from prominent members in the statistics community. This writeup was prepared before I had a chance to read the paper, but I hope it covers some of the principles and recommendations. And if not, like statistical models, the way I do data analysis will iterate and improve.

“Practical Bayesian data analysis, like all data analysis, is an iterative process of model building, inference, model checking and evaluation, and model expansion” - Visualisation Bayesian Workflow - Gabry, Simpson, Vehtari, Betancourt, Gelman (2019)

The proposed workflow I adopted was originally inspired from blog posts by Jim Savage a few years ago and more recently, Monica Alexander’s example of visualisation in an end-to-end bayesian analysis. I’ve included a full list of resources which helped me at the end of this post. The steps in bold will be discussed below while an application using the full workflow will be in an upcoming writeup.

Steps in proposed workflow

Exploratory data analysis and data transformation
Write out full probability model
Prior predictive checks - simulate data from the implied generative model
Fit model on fake data - can we recover the known parameters?
Estimate model on real data
Check whether MCMC sampler ran efficiently and model convergence
Posterior predictive check to evaluate model fit
Model selection using cross validation and information criteria
Optional: Evaluate model performance on test or out of sample dataset (not strictly necessary if the modelling task is not a predictive problem)

Predicting housing prices

1) Exploratory data analysis and data transformation

The full dataset for this competition contains 79 features to predict the target variable SalesPrice. For this exercise I will focus on two variables: Neighbourhood (categorical: physical locations within Ames city limits) and LotArea (positive real: lot size in square feet). I chose these variables as they are consistent with my understanding of how housing prices vary in relation to their location and property size.

Aside: The model and feature selection in this example are deliberately simple. The goal is to motivate workflow, diagnostics and to interrogate assumptions, so I only used two variables to make it easier to follow. My repo contains examples of other models and additional features.

import pystan
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
import arviz as az
import math

az.style.use('arviz-darkgrid')

df = pd.read_csv('data/train.csv').loc[:, ['SalePrice', 'LotArea', 'Neighborhood']]

# Log transform
df['log_sales_price'] = np.log(df['SalePrice'])
df['log_lot_area'] = np.log(df['LotArea'])

# Create numerical categories (add 1 due to zero indexing)
df['neighbourhood'] = df['Neighborhood'].astype('category').cat.codes+1

df.head().style

	SalePrice	LotArea	Neighborhood	log_sales_price	log_lot_area	neighbourhood
0	208500	8450	CollgCr	12.247694	9.041922	6
1	181500	9600	Veenker	12.109011	9.169518	25
2	223500	11250	CollgCr	12.317167	9.328123	6
3	140000	9550	Crawfor	11.849398	9.164296	7
4	250000	14260	NoRidge	12.429216	9.565214	16

A scatter plot shows a positive correlation between log(SalePrice) and log(LotArea). Fitting OLS on the logarithms of both variables assumes a linear relationship on the multiplicative scale. All else equal, property prices tend to be higher with larger lot sizes. However, this univariate linear model clearly underfits the data and there are almost surely unobserved confounding variables.

sns.lmplot(x='log_lot_area',y='log_sales_price',data=df,fit_reg=True, ci = False)
plt.tight_layout()

A potential reason for underfitting may be some neighbourhoods have higher average prices than other neighbourhoods (which would result in different intercepts). Furthermore, the association between housing prices and lot size may depend on different neighbourhoods as well (varying slopes). This variation could be driven by different zonings or housing densities within neighbourhoods that could impact the relationship between lot size and prices. Splitting the plot out by neighbourhood displays the heterogeneity in linear trends.

facet_scatter = sns.lmplot(x="log_lot_area", 
                           y="log_sales_price", 
                           col="Neighborhood",
                           col_wrap = 5,
                           data=df,
                           ci = None, 
                           truncate=False,
                           col_order = sorted(df['Neighborhood'].drop_duplicates()))

facet_scatter.set(xlim=(5, 15))
facet_scatter.set(ylim=(5, 15))

We can see variation in the slopes and intercepts as well as imbalanced sampling between neighbourhood clusters. This and other unobserved confounders probably contributed to some of the weak/negative gradients. The small sample sizes in some neighbourhoods will be prone to overfitting and will give noisy estimates which will require regularisation.

2) Write out full probability model

3 basic linear models can be used to approach this problem:

Pooled OLS (assumes all observations come from “one neighbourhood”, equivalent to the OLS model in the first scatterplot)
No pooling OLS (conceptually the same as a dummy variable regression - assumes independence between all neighbourhoods)
Saturated regression (adds interactive effects between log(LotArea)_i and neighbourhood to no pooling OLS)

I will use no pooling OLS to demonstrate the rest of the workflow. There is definitely room for improving these models. In fact, this problem is a good candidate for multilevel models. They allow for information to be borrowed between neighbourhood clusters through partial pooling and removes the assumption of independence. This will help regularise the effects of small and imbalanced sample sizes across neighbourhood. I will apply the full workflow using multilevel models in the next post.

Model specification

The no pooling regression is written out below, where \(i\) indexes the property and \(j\) indexes each neighbourhood. I’ve assigned a gaussian likelihood which assumes that the residuals are normally distributed.

\[ \begin{align} y_i &\sim Normal(\mu_i, \sigma) \\ \mu_i &= \alpha_{j} + \beta * x_i \\ \end{align} \] Where \(y_i\) is log(SalesPrice) and \(x_i\) is log(LotArea) scaled to mean 0 and standard deviation 1. \(\alpha_j\) is an intercept parameter for the jth neighbourhood in the sample. The slope coefficient can be interpreted as: a one standard deviation increase in log(LotArea) is a \(\beta\) standard deviation change in log(SalesPrice).

# Standardise predictors
def z_std(x):
    """
    Centres at mean 0 and standard deviation 1
    """
    z_score = (x - x.mean()) / x.std()
    return(z_score)
    
# Center and scale predictor
df['log_lot_area_z'] = z_std(df['log_lot_area'])

# Scale target
df['log_sales_price_z'] = z_std(df['log_sales_price'])

\[ \begin{align} y_i &= \frac{log(SalesPrice)_i - \overline{log(SalesPrice)}}{\sigma_{log(SalesPrice)}} \\ x_i &= \frac{log(LotArea)_i - \overline{log(LotArea)}}{\sigma_{log(LotArea)}} \end{align} \]

Standardising both outcome and predictor variables makes sampling from the posterior distribution easier when we fit the model. If we had more continuous regressors, we could also compare the parameters on the same scale. Standardising also plays an important role in setting priors as we’ll see below.

Selecting priors

Probability distributions need to be assigned to the parameters for this to be a bayesian model. Setting priors is an opportunity to encode domain knowledge or results from related studies into the model. Unfortunately, I do not have much domain expertise or information about the context of this dataset to give very informative priors. So I have chosen to use weakly informative priors following the advice of the Stan developers. This will help me regularise model predictions within the plausible outcome space.

For \(\beta\) I’ll assign a \(Normal(0, 1)\) which puts ~95% of the probability between two standard deviations for a unit increase in \(x\). We want to hedge against overfitting by shrinking the coefficient towards zero. This is achieved by putting probability mass on all plausible values of \(\beta\) with less weight on extreme relationships.

\(\alpha_j\) is the intercept for the \(j^{th}\) neighbourhood. In a pooled OLS regression between price and lot area, the intercept \(\alpha\) (ignoring the neighbourhood means ignoring the j subscript) would be interpreted as the value of \(y\) when \(x\) is 0. Since \(x\) has a mean of zero, \(\alpha\) has the additional interpretation as the value of \(y\) when \(x\) is equal to its sample mean. By construction, \(\alpha\) must be 0, the sample mean of \(y\).

So in the case of \(\alpha_j\) I set a normal prior with a mean of 0 and a standard deviation of 1 for all neighbourhoods, regularising neighbourhood effects within two standard deviations of the grand mean of \(y\).

The variance parameter \(\sigma\) is defined over positive real numbers. So our prior should only put probabilistic weight on positive values. In this case I’ve chosen a weakly regularising \(exponential(1)\) prior. Other candidate priors are the Half-Cauchy distribution or the Half-Normal which has thinner tails.

These weakly informative priors express my belief that the parameters of this model would overfit the sample and that we need to regularise their effects. Standardising the variables made this job much easier and intuitive. All together the full model looks like:

\[ \begin{align} y_i &\sim Normal(\mu_i, \sigma) \\ \mu_i &= \alpha_{j} + \beta * x_i \\ \alpha_j &\sim Normal(0, 1)\\ \beta &\sim Normal(0, 1) \\ \sigma &\sim exp(1) \end{align} \]

3) Prior predictive checks - simulate data from the implied generative model

Prior predictive checks are useful for understanding the implications of our priors. Parameters are simulated from the joint prior distribution and visualised to see the implied relationships between the target and predictor variables. This will help diagnose any problems with our assumptions and modelling decisions. These checks become more important for generalised linear models since the outcome and parameter space are different due to the link function. For example, priors on parameters in a logistic regression are in the log-odds space and may behave differently to our expectations on the outcome space.

The code below includes all the inputs necessary to estimate the model on the data. Setting run_estimation = 0 means Stan will only simulate values from the joint prior distribution since the likelihood is not evaluated (thanks to Jim for this handy tip).

no_pooling_stan_code = '''
// No pooling model for predicting housing prices
data {
    // Fitting the model on training data
    int<lower=0> N; // Number of rows
    int<lower=0> neighbourhood[N]; // neighbourhood categorical variable
    int<lower=0> N_neighbourhood; // number of neighbourhood categories
    vector[N] log_sales_price; // log sales price
    vector[N] log_lot_area; // log lot area

    // Adjust scale parameters in python
    real alpha_sd;
    real beta_sd;
    
    // Set to zero for prior predictive checks, set to one to evaluate likelihood
    int<lower = 0, upper = 1> run_estimation;
}
parameters {
    vector[N_neighbourhood] alpha; // Vector of alpha coefficients for each neighbourhood
    real beta;
    real<lower=0> sigma;
}
model {
    // Priors
    target += normal_lpdf(alpha | 0, alpha_sd);
    target += normal_lpdf(beta | 0, beta_sd);
    target += exponential_lpdf(sigma |1);
    
    // Likelihood
    if(run_estimation==1){
        target += normal_lpdf(log_sales_price | alpha[neighbourhood] + beta * log_lot_area, sigma);

    }
}
generated quantities {
    // Uses fitted model to generate values of interest
    vector[N] log_lik; // Log likelihood
    vector[N] y_hat; // Predictions using training data
    {
    for(n in 1:N){
          log_lik[n] = normal_lpdf(log_sales_price | alpha[neighbourhood[n]] + beta * log_lot_area[n], sigma);
          y_hat[n] = normal_rng(alpha[neighbourhood[n]] + beta * log_lot_area[n], sigma);      
        }
    }
}
'''

# Dictionary contains all data inputs
npm_data_check = dict(N = len(df),
                      log_sales_price = df['log_sales_price_z'],
                      log_lot_area = df['log_lot_area_z'],
                      neighbourhood = df['neighbourhood'],
                      N_neighbourhood = len(df['neighbourhood'].unique()),
                      alpha_sd = 1, 
                      beta_sd = 1, 
                      run_estimation = 0)

# Compile stan model
no_pooling_model = pystan.StanModel(model_code = no_pooling_stan_code)

# Draw samples from joint prior distribution
fit_npm_check = no_pooling_model.sampling(data=npm_data_check, seed = 12345)

# Extract samples into a pandas dataframe
npm_df_check = fit_npm_check.to_dataframe()

For the prior predictive checks, we recommend not cleaving too closely to the observed data and instead aiming for a prior data generating process that can produce plausible data sets, not necessarily ones that are indistinguishable from observed data. - Visualisation Bayesian Workflow - Gabry, Simpson, Vehtari, Betancourt, Gelman (2019)

The implied predictions of our priors are visualised below. I’ve arbitrarily chosen the 4th neighbourhood index (\(\alpha_{j=4}\)) since the priors for the neighbourhoods are the same. Weakly informative priors should create bounds between possible values while allowing for some implausible relationships. Remembering that 95% of gaussian mass exists within two standard deviations of the mean is a useful guide for determining what is reasonable.

Let’s see an example of setting uninformative priors and its implications of the data generating process. I’ve set the scale parameters for \(\alpha\) and \(\beta\) to be 10 which are quite diffuse. The implied predictions of the mean are much wider and well beyond the minimum and maximum values in the real data. This suggests that the model is giving too much probabilistic weight to highly implausible datasets.

npm_data_check_wide = dict(N = len(df),
                      log_sales_price = df['log_sales_price_z'],
                      log_lot_area = df['log_lot_area_z'],
                      neighbourhood = df['neighbourhood'],
                      N_neighbourhood = len(df['Neighborhood'].unique()),
                      alpha_sd = 10, 
                      beta_sd = 10, 
                      run_estimation = 0)

fit_npm_check_wide = no_pooling_model.sampling(data=npm_data_check_wide)
npm_df_check_wide = fit_npm_check_wide.to_dataframe()

_, ax = plt.subplots(figsize = (13, 8))

x = np.linspace(-3, 3, 200)

for alpha, beta in zip(npm_df_check_wide["alpha[4]"][:100], npm_df_check_wide["beta"][:100]):
    y = alpha + beta * x
    ax.plot(x, y, c="k", alpha=0.4)

ax.set_xlabel("x (z-scores)")
ax.set_ylabel("Fitted y (z-scores)")
ax.set_title("Prior predictive checks -- Uninformative (flat) priors");

Our original scale parameters of 1 produce more reasonable relationships. There are still some extreme regression lines implied by our data generating process, but they are bound to more realistic outcomes relative to the diffuse priors.

_, ax = plt.subplots(figsize = (13, 8))

x = np.linspace(-3, 3, 200)

for alpha, beta in zip(npm_df_check["alpha[4]"][:100], npm_df_check["beta"][:100]):
    y = alpha + beta * x
    ax.plot(x, y, c="blue", alpha=0.4)

ax.set_xlabel("x (z-scores)")
ax.set_ylabel("Fitted y (z-scores)")
ax.set_title("Prior predictive checks -- Weakly regularizing priors")

Putting both sets of lines on the same scale emphasises the difference in simulated values. The blue lines from the previous graph cover a tighter space relative to the simulations from the uninformative priors.

# Putting both on the same scale
_, ax = plt.subplots(figsize = (13, 8))

for alpha_wide, beta_wide in zip(npm_df_check_wide["alpha[4]"][:100], npm_df_check_wide["beta"][:100]):
    y_wide = alpha_wide + beta_wide * x
    ax.plot(x, y_wide, c="k", alpha=0.4)
    
for alpha, beta in zip(npm_df_check["alpha[4]"][:100], npm_df_check["beta"][:100]):
    y = alpha + beta * x
    ax.plot(x, y, c="blue", alpha=0.2)

ax.set_xlabel("x (z-scores)")
ax.set_ylabel("Fitted y (z-scores)")
ax.set_title("Prior predictive checks -- Uninformative (black) vs weakly informative (blue)")

4) Fit model on fake data

We can use the simulations to see if our model can successfully estimate the parameters used to generate fake data (the implied \(\hat{y}\)). Take a draw from the prior samples (e.g. the 50th simulation) and estimate the model on the data produced by these parameters. Let’s see if the model fitted on fake data can capture the “true” parameters (dotted red lines) of the data generating process. If the model cannot capture the known parameters which generated fake data, there is no certainty it will be estimating the correct parameters on real data.

# Pick random simulation, let's say 50
random_draw = 50

# Extract the simulated (fake) data implied by the parameters in sample 50
y_sim = npm_df_check.filter(regex = 'y_hat').iloc[random_draw, :]

# Extract the parameters corresponding to sample 10
true_parameters = npm_df_check.filter(regex = 'alpha|beta|sigma').iloc[random_draw, :]

# Fit the model on the fake data
_npm_data_check = dict(N = len(df),
              log_sales_price = y_sim, # this is now fitting on the extracted fake data in sample 50
              log_lot_area = df['log_lot_area_z'],
              neighbourhood = df['neighbourhood'],
              N_neighbourhood = len(df['Neighborhood'].unique()),
              alpha_sd = 1, 
              beta_sd = 1, 
              run_estimation = 1)

_fit_npm_check = no_pooling_model.sampling(data=_npm_data_check, seed = 12345)
_npm_df_check = _fit_npm_check.to_dataframe()
fake_fit = _npm_df_check.filter(regex = 'alpha|beta|sigma')
parameter_df = pd.melt(fake_fit)

# Plot will give distributions of all parameters to see if it can capture the known parameters
fig, axes = plt.subplots(nrows=max(2, math.ceil(fake_fit.shape[1] / 6)), ncols=6, sharex=False, sharey = False, figsize=(21,13))
fig.suptitle('Model Checking - red lines are "true" parameters', size = 30)
axes_list = [item for sublist in axes for item in sublist] 
parameters = parameter_df[['variable']].drop_duplicates().set_index('variable').index
grouped = parameter_df.groupby("variable")

for parameter in parameters:
    selection = grouped.get_group(parameter)
    ax = axes_list.pop(0)
    selection.plot.kde(label=parameter, ax=ax, legend=False)
    ax.set_title(parameter)
    ax.grid(linewidth=0.25)
    ax.axvline(x=true_parameters[parameter], color='red', linestyle='--', alpha = 0.5)

# Now use the matplotlib .remove() method to delete anything we didn't use
for ax in axes_list:
    ax.remove()

plt.tight_layout()

The model sufficiently captured the known parameters. The next post will go through a more interesting example where this fails and requires us to rethink how we specified our models.

5) Estimate model on real data

Set run_estimation=1 and run the code to fit the model. Stan will sample the joint posterior distribution using the default Markov chain Monte Carlo (MCMC) algorithm, the No-U-Turn sampler (NUTs).

# Dictionary with data inputs - set run_estimation=1
npm_data = dict(N = len(df),
              log_sales_price = df['log_sales_price_z'],
              log_lot_area = df['log_lot_area_z'],
              neighbourhood = df['neighbourhood'],
              N_neighbourhood = len(df['Neighborhood'].unique()),
              alpha_sd = 1, 
              beta_sd = 1, 
              run_estimation = 1)

# Fit model by sampling from posterior distribution
fit_npm = no_pooling_model.sampling(data=npm_data)

# For generating visualisations using the arviz package
npm_az = az.from_pystan(
    posterior=fit_npm,
    posterior_predictive="y_hat",
    observed_data="log_sales_price",
    log_likelihood='log_lik',
)

# Extract samples into dataframe
fit_npm_df = fit_npm.to_dataframe()

6) Check whether MCMC sampler and model fit

Stan won’t have trouble sampling from such a simple model, so I won’t go through chain diagnostics in detail. I’ve included number of effective samples and Rhat diagnostics for completeness. We can see the posterior distributions of all the parameters by looking at the traceplot as well.

Traceplot

# Inspect model fit
az.plot_trace(fit_npm, 
              var_names=["alpha", "beta", "sigma"], 
              compact = True, 
              chain_prop = 'color')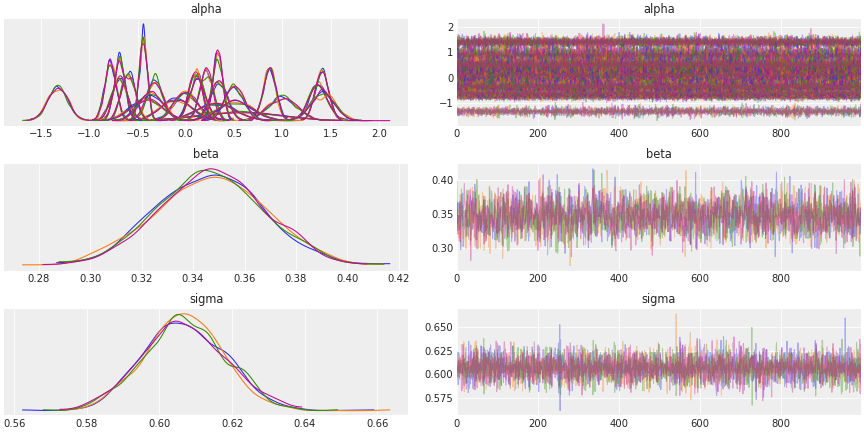

Posterior distributions

# Inspect model fit
axes = az.plot_forest(fit_npm, 
              var_names=["alpha", "beta", "sigma"],
              combined = True)

axes[0].set_title('Posterior distributions of fitted parameters')

neff / Rhat

print(pystan.stansummary(fit_npm, 
                         pars=['alpha', 'beta', 'sigma'], 
                         probs=(0.025, 0.50, 0.975), 
                         digits_summary=3))

Inference for Stan model: anon_model_9d4f76eb27d91c6b75464a26e0b032c7.
4 chains, each with iter=2000; warmup=1000; thin=1;
post-warmup draws per chain=1000, total post-warmup draws=4000.

            mean se_mean     sd   2.5%    50%  97.5%  n_eff   Rhat
alpha[1]   1.004   0.002  0.148   0.71  1.004  1.288   6313  0.999
alpha[2]   0.565   0.005  0.401 -0.211  0.564  1.334   6117  0.999
alpha[3]  -0.102   0.002  0.162 -0.412 -0.102  0.212   4685    1.0
alpha[4]  -0.686 9.71e-4  0.082 -0.845 -0.686 -0.523   7060    1.0
alpha[5]   0.003   0.002  0.121 -0.2292.25e-4  0.245   6299    1.0
alpha[6]    0.33 5.69e-4  0.051  0.229   0.33  0.429   7894  0.999
alpha[7]    0.34   0.001  0.087  0.169  0.339  0.507   7475    1.0
alpha[8]   -0.78 6.89e-4  0.059 -0.895 -0.781 -0.664   7357    1.0
alpha[9]   0.215 9.01e-4  0.068  0.082  0.215   0.35   5743  0.999
alpha[10] -1.328   0.001  0.101 -1.525 -1.329 -1.132   7365    1.0
alpha[11]  -0.41   0.002  0.159 -0.715 -0.408 -0.105   5670    1.0
alpha[12] -0.319 9.71e-4  0.087 -0.496  -0.32 -0.142   8023  0.999
alpha[13]  -0.44 4.84e-4  0.041  -0.52  -0.44 -0.362   7346  0.999
alpha[14]  0.312   0.002  0.202 -0.087  0.313  0.714   7154  0.999
alpha[15]    0.1 8.56e-4  0.071  -0.04    0.1   0.24   6834  0.999
alpha[16]   1.37   0.001  0.095  1.181  1.369  1.561   6408    1.0
alpha[17]  1.412 8.08e-4  0.068  1.277  1.412  1.546   7174  0.999
alpha[18] -0.685 6.69e-4  0.057 -0.797 -0.685  -0.57   7138  0.999
alpha[19] -0.362   0.001  0.122 -0.598 -0.362 -0.127   7838    1.0
alpha[20] -0.597 7.55e-4  0.071 -0.733 -0.597 -0.456   8863  0.999
alpha[21]  0.121  9.7e-4  0.079 -0.036   0.12  0.274   6678  0.999
alpha[22]  0.869 7.96e-4  0.066  0.739  0.869  0.995   6790    1.0
alpha[23]   1.42   0.001  0.123  1.176  1.421  1.659   7563    1.0
alpha[24]  0.503   0.001  0.099   0.31  0.501  0.699   7092    1.0
alpha[25]  0.515   0.002  0.179  0.167  0.515  0.868   7366  0.999
beta       0.347 3.71e-4  0.021  0.307  0.347  0.387   3126  0.999
sigma      0.607 1.37e-4  0.011  0.586  0.607  0.629   6687  0.999

Samples were drawn using NUTS at Thu Nov 12 11:48:18 2020.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at 
convergence, Rhat=1).

7) Posterior predictive check to evaluate model performance

How well did the model perform? We can perform posterior predictive checks to see if sampled distributions from the fitted model can approximate the density of SalesPrice. If the model performs well, it should be able to retrodict the density of the data used to train the model. The blue lines are the predictions drawn from the joint posterior distribution compared with the observed density of the target \(y\) variable.

# Select 300 samples to plot against observed distribution
az.plot_ppc(data = npm_az, 
            kind = 'kde', 
            data_pairs = {'log_sales_price' : 'y_hat'},
            legend = True,
            color='cyan',
            mean = False,
            figsize=(8, 5),
            alpha = 0.5,
            num_pp_samples=300)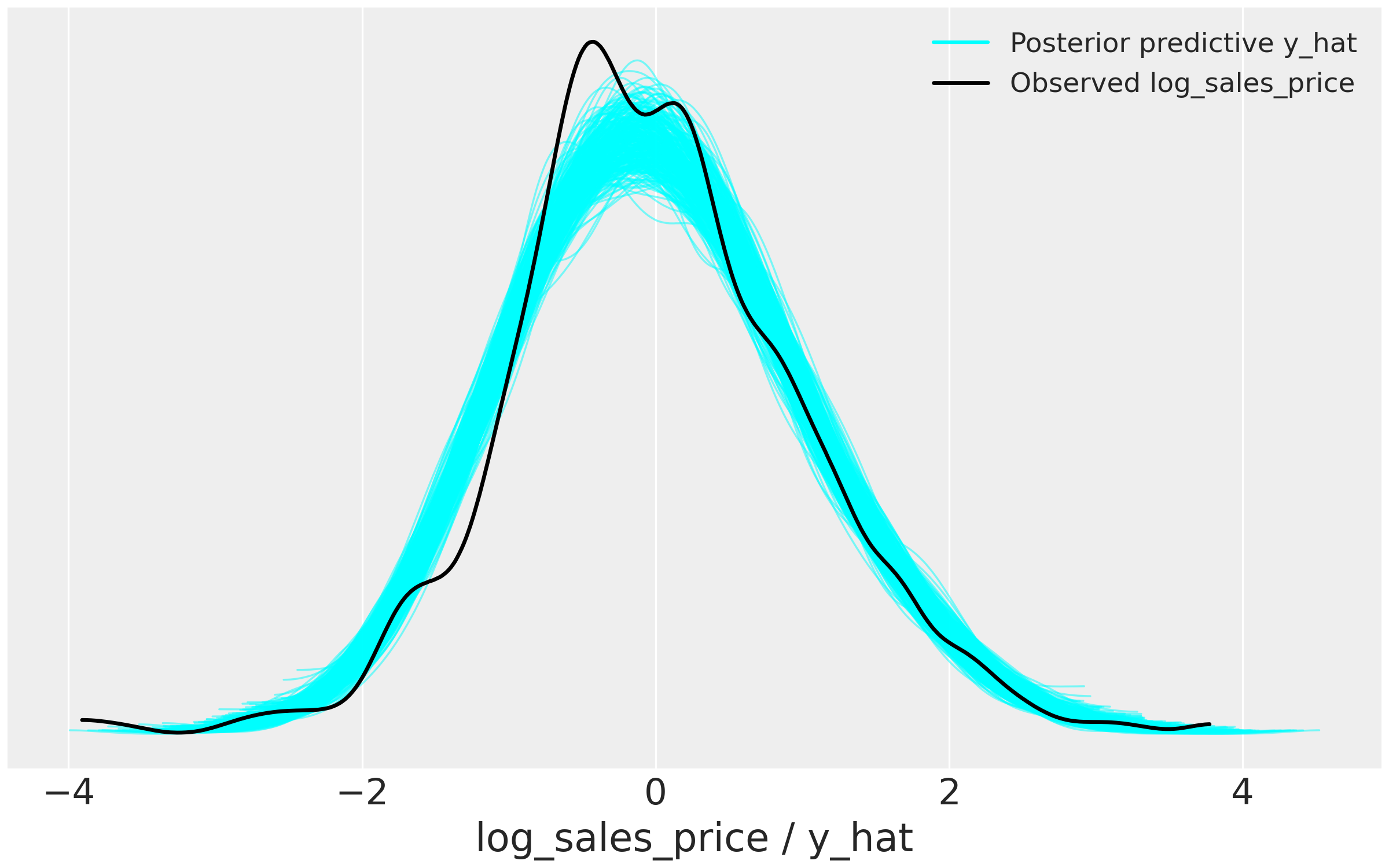

Reversing the data transformations gives back the posterior predictive checks on the natural scale (rescale \(y\) and exponentiate log(SalesPrice) to get back SalesPrice):

fig, axes = pl#| t.subplots(1,1, figsize = (13, 8))
np.exp(fit_npm_df.filter(regex = 'y_hat')*df['log_sales_price'].std()+df['log_sales_price'].mean())\
                 .T\
                 .iloc[:, :300]\
                 .plot.kde(legend = False, 
                           title = 'Posterior predictive Checks - Black: Observed Sale Price, blue: posterior samples', 
                           xlim = (30000,500000),
                           alpha = 0.08,
                           ax = axes, color = 'aqua');

df['SalePrice'].plot.kde(legend = False, 
                         xlim = (30000,500000),
                         alpha = 1,
                         ax = axes,
                         color = 'black');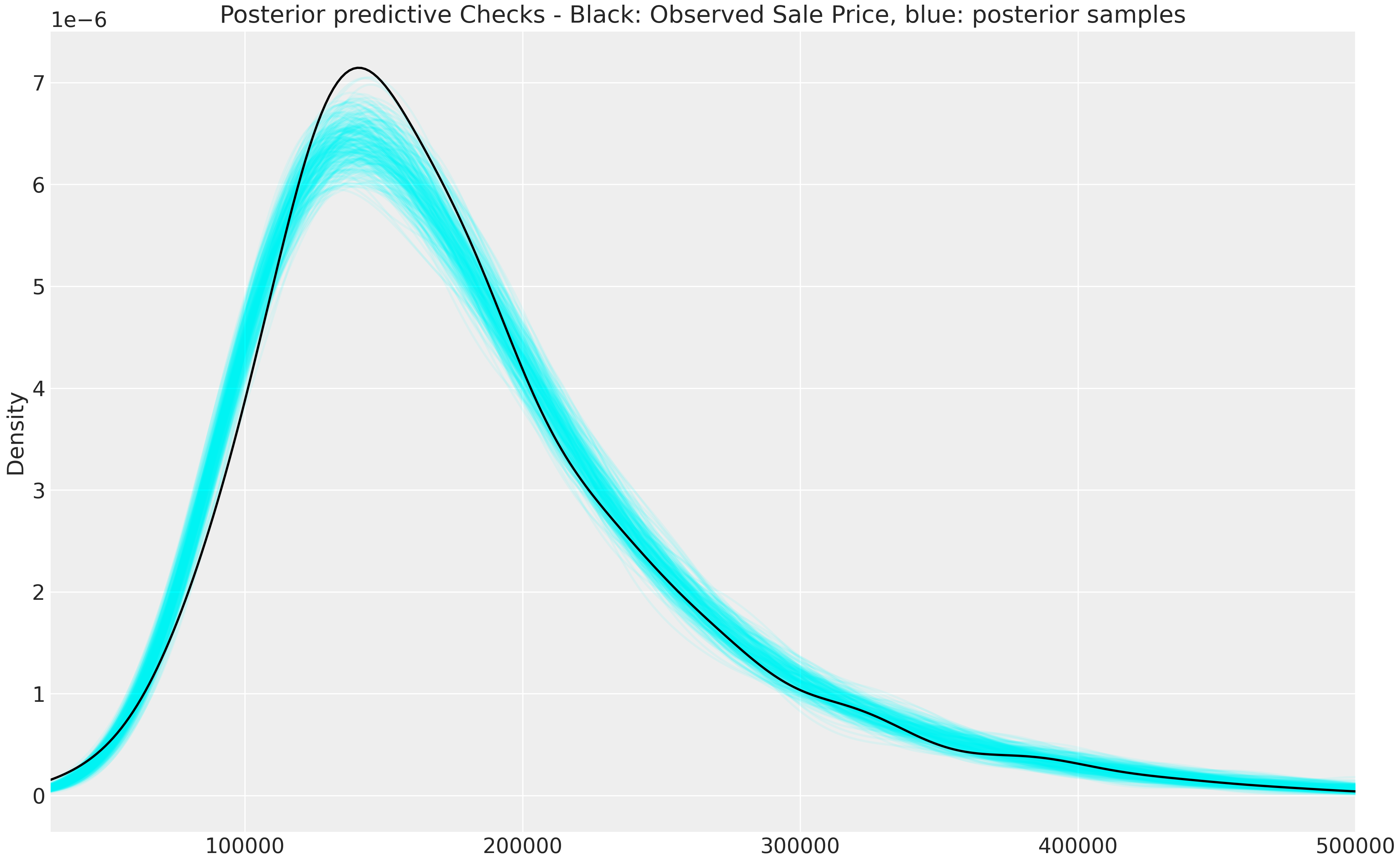

Not bad for a simple model. There is definitely room for iteration and improvement.

1) Exploratory data analysis and data transformation

library(tidyverse)
library(rstan)
library(bayesplot)

# Detect cores for parallel sampling
options(mc.cores = parallel::detectCores())

# Load data, select variables, apply log transformation
df <-  read_csv('data/train.csv') %>% 
  select('SalePrice', 'LotArea', 'Neighborhood')%>% 
  mutate(log_sales_price = log(SalePrice),
         log_lot_area = log(LotArea),
         neighbourhood = as.integer(as.factor(Neighborhood)))
head(df)

ggplot(df, aes(x = log_lot_area, y = log_sales_price)) +
  geom_point(colour = 'blue') +
  geom_smooth(method = lm, se = FALSE, formula = 'y ~ x') + 
  ggsave('figures/2r_pooling_scatter.png', dpi = 300, width=10, height = 8, units = 'in')

ggplot(df, aes(x = log_lot_area, y = log_sales_price)) +
  geom_point(colour = 'blue') +
  geom_smooth(method = lm, se = FALSE, formula = 'y ~ x', fullrange = TRUE) +
  facet_wrap(~Neighborhood) +
  theme(strip.background = element_blank())

2) Write out full probability model

3 basic linear models can be used to approach this problem:

Pooled OLS (assumes all observations come from “one neighbourhood”, equivalent to the OLS model in the first scatterplot)
No pooling OLS (conceptually the same as a dummy variable regression - assumes independence between all neighbourhoods)
Saturated regression (adds interactive effects between log(LotArea)_i and neighbourhood to no pooling OLS)

Model specification

df  <-  df %>% mutate(log_lot_area_z = scale(log_lot_area),
                    log_sales_price_z = scale(log_sales_price))

\[ \begin{align} y_i &= \frac{log(SalesPrice)_i - \overline{log(SalesPrice)}}{\sigma_{log(SalesPrice)}} \\ x_i &= \frac{log(LotArea)_i - \overline{log(LotArea)}}{\sigma_{log(LotArea)}} \end{align} \] Standardising both outcome and predictor variables makes sampling from the posterior distribution easier when we fit the model. If we had more continuous regressors, we could also compare the parameters on the same scale. Standardising also plays an important role in setting priors as we’ll see below.

Selecting priors

\[ \begin{align} y_i &\sim Normal(\mu_i, \sigma) \\ \mu_i &= \alpha_{j} + \beta * x_i \\ \alpha_j &\sim Normal(0, 1)\\ \beta &\sim Normal(0, 1) \\ \sigma &\sim exp(1) \end{align} \]

3) Prior predictive checks - simulate fake data from the implied generative model

no_pooling_stan_code = "
// No pooling model for predicting housing prices
data {
    // Fitting the model on training data
    int<lower=0> N; // Number of rows
    int<lower=0> neighbourhood[N]; // neighbourhood categorical variable
    int<lower=0> N_neighbourhood; // number of neighbourhood categories
    vector[N] log_sales_price; // log sales price
    vector[N] log_lot_area; // log lot area

    // Adjust scale parameters in python
    real alpha_sd;
    real beta_sd;
    
    // Set to zero for prior predictive checks, set to one to evaluate likelihood
    int<lower = 0, upper = 1> run_estimation;
}
parameters {
    vector[N_neighbourhood] alpha; // Vector of alpha coefficients for each neighbourhood
    real beta;
    real<lower=0> sigma;
}
model {
    // Priors
    target += normal_lpdf(alpha | 0, alpha_sd);
    target += normal_lpdf(beta | 0, beta_sd);
    target += exponential_lpdf(sigma |1);
    //target += normal_lpdf(sigma |0, 1);
    
    // Likelihood
    if(run_estimation==1){
        target += normal_lpdf(log_sales_price | alpha[neighbourhood] + beta * log_lot_area, sigma);

    }
}
generated quantities {
    // Uses fitted model to generate values of interest without re running the sampler
    vector[N] log_lik; // Log likelihood
    vector[N] y_hat; // Predictions using training data
    {
    for(n in 1:N){
          log_lik[n] = normal_lpdf(log_sales_price | alpha[neighbourhood[n]] + beta * log_lot_area[n], sigma);
          y_hat[n] = normal_rng(alpha[neighbourhood[n]] + beta * log_lot_area[n], sigma);      
        }
    }
}
"

# List contains all data inputs
npm_data_check = list(N = nrow(df),
                      log_sales_price = as.vector(df$log_sales_price_z),
                      log_lot_area = as.vector(df$log_lot_area_z),
                      neighbourhood = as.vector(df$neighbourhood),
                      N_neighbourhood = max(df$neighbourhood),
                      alpha_sd = 1, 
                      beta_sd = 1, 
                      run_estimation = 0)

# Draw samples from joint prior distribution
fit_npm_check = stan(model_code = no_pooling_stan_code, data = npm_data_check, chains = 4, seed = 12345)

# Extract samples into a pandas dataframe
npm_df_check = as.data.frame(fit_npm_check)

For the prior predictive checks, we recommend not cleaving too closely to the observed data and instead aiming for a prior data generating process that can produce plausible data sets, not necessarily ones that are indistinguishable from observed data. - Visualisation Bayesian Workflow - Gabry, Simpson, Vehtari, Betancourt, Gelman (2019)

# Fit model with diffuse priors
npm_data_check_wide = list(N = nrow(df),
                      log_sales_price = as.vector(df$log_sales_price_z),
                      log_lot_area = as.vector(df$log_lot_area_z),
                      neighbourhood = as.vector(df$neighbourhood),
                      N_neighbourhood = max(df$neighbourhood),
                      alpha_sd = 10, 
                      beta_sd = 10, 
                      run_estimation = 0)

fit_npm_check_wide = stan(model_code = no_pooling_stan_code, data=npm_data_check_wide, chains = 4, seed = 12345)
npm_df_check_wide = as.data.frame(fit_npm_check_wide)

# Create length of std x variables
x <- seq(from = -3, to = 3, length.out = 200)

# Create empty dataframe and fill it with parameters
df_wide <- as.data.frame(matrix(ncol=100, nrow=200))
for (i in 1:100) {
  alpha <- npm_df_check_wide$`alpha[4]`[i]
  beta <- npm_df_check_wide$beta[i]
  df_wide[, i] <- alpha + beta * x
  
}

# Tidy up filled dataframe
df_wide <- df_wide %>% mutate(x = x) %>% pivot_longer(starts_with("V"))

# Plot
ggplot(df_wide, aes(x = x, y = value)) +
  geom_line(aes(group = name), size = 0.2) +
  scale_x_continuous(breaks = seq(-3, 3, 1)) +
  labs(title = 'Prior predictive checks -- Uninformative (flat) priors',
             x = 'x (z-scores)',
             y = 'Fitted y (z_scores)')

# Create length of std x variables
x <- seq(from = -3, to = 3, length.out = 200)

# Create empty dataframe and fill it with parameters
df_regularising <- as.data.frame(matrix(ncol=100, nrow=200))
for (i in 1:100) {
  alpha <- npm_df_check$`alpha[4]`[i]
  beta <- npm_df_check$beta[i]
  df_regularising[, i] <- alpha + beta * x
  
}

# Tidy up filled dataframe
df_regularising <- df_regularising %>% mutate(x = x) %>% pivot_longer(starts_with("V"))

# Plot
ggplot(df_regularising, aes(x = x, y = value)) +
  geom_line(aes(group = name), size = 0.2) +
  scale_x_continuous(breaks = seq(-3, 3, 1)) +
  labs(title = 'Prior predictive checks -- Weakly regularizing priors',
             x = 'x (z-scores)',
             y = 'Fitted y (z_scores)')

ggplot(df_wide, aes(x = x, y = value)) +
  geom_line(aes(group = name), size = 0.2) +
  geom_line(data = df_regularising, aes(group = name), size = 0.2, colour = 'blue') +
  scale_x_continuous(breaks = seq(-3, 3, 1)) +
  labs(title = 'Prior predictive checks -- Uninformative (flat) priors',
             x = 'x (z-scores)',
             y = 'Fitted y (z_scores)')

4) Fit model on fake data

# Pick random simulation, let's say 50
random_draw <- 50

# Extract the simulated (fake) data implied by the parameters in sample 50
y_sim <-  npm_df_check[random_draw, ] %>% select(contains('y_hat')) %>% t()

# Extract the parameters corresponding to sample 50
true_parameters = npm_df_check[random_draw,] %>% select(contains(c('alpha','beta','sigma')))

# List contains all data inputs
npm_data_check_ = list(N = nrow(df),
                      log_sales_price = as.vector(y_sim), # target is now extracted fake data in sample 50
                      log_lot_area = as.vector(df$log_lot_area_z),
                      neighbourhood = as.vector(df$neighbourhood),
                      N_neighbourhood = max(df$neighbourhood),
                      alpha_sd = 1, 
                      beta_sd = 1, 
                      run_estimation = 1)

# Fit the model on the fake data
fit_npm_check_ = stan(model_code = no_pooling_stan_code, data=npm_data_check_, chains = 4, seed = 12345)
npm_df_check_ = as.data.frame(fit_npm_check_)

# Extract parameters and tidy dataframe
fake_fit = npm_df_check_ %>% select(contains(c('alpha', 'beta', 'sigma')))
parameter_df = fake_fit %>% pivot_longer(everything()) %>% rename(parameters = name)
parameter_df$parameters <- factor(parameter_df$parameters, levels = (parameter_df$parameters %>% unique()))

# Plot will give distributions of all parameters to see if it can capture the known parameters
ggplot(parameter_df, aes(value)) + 
  geom_density(colour = 'blue') + 
  facet_wrap(~parameters, scales = 'free') + 
  geom_vline(data = (true_parameters %>% pivot_longer(everything()) %>% rename(parameters = name)), aes(xintercept = value), colour = 'red') + 
  labs(title = 'Model Checking - red lines are "true" parameters',
       x = '') + 
  theme(strip.background = element_blank())

5) Estimate model on real data

Set run_estimation=1 and run the code to fit the model. Stan will sample the joint posterior distribution using the default Markov chain Monte Carlo (MCMC) algorithm, the No-U-Turn sampler (NUTs).

# Dictionary with data inputs - set run_estimation=1
npm_data = list(N = nrow(df),
                      log_sales_price = as.vector(df$log_sales_price_z),
                      log_lot_area = as.vector(df$log_lot_area_z),
                      neighbourhood = as.vector(df$neighbourhood),
                      N_neighbourhood = max(df$neighbourhood),
                      alpha_sd = 1, 
                      beta_sd = 1, 
                      run_estimation = 1)

# Fit model by sampling from posterior distribution
fit_npm = stan(model_code = no_pooling_stan_code, data = npm_data, chains = 4, seed = 12345)

# Extract samples into dataframe
fit_npm_df = as.data.frame(fit_npm)

6) Check whether MCMC sampler and model fit

Traceplot

# Inspect model fit
color_scheme_set("mix-blue-red")

mcmc_combo(
 as.array(fit_npm),
 combo = c("dens_overlay", "trace"),
 pars = c('alpha[1]', 'beta', 'sigma'),
 gg_theme = legend_none())

Posterior distributions

stan_plot(fit_npm, 
          show_density = FALSE, 
          unconstrain = TRUE, 
          pars = c('alpha', 'beta', 'sigma')) + 
  labs(title = 'Posterior distributions of fitted parameters')

neff / Rhat

print(fit_npm, pars = c('alpha', 'beta', 'sigma'), 
                         probs=c(0.025, 0.50, 0.975), 
                         digits_summary=3)

Inference for Stan model: 2be0e54fe1314f469f9b784aa4444aba.
4 chains, each with iter=2000; warmup=1000; thin=1; 
post-warmup draws per chain=1000, total post-warmup draws=4000.

            mean se_mean    sd   2.5%    50%  97.5% n_eff  Rhat
alpha[1]   1.005   0.002 0.148  0.708  1.007  1.291  5778 1.000
alpha[2]   0.565   0.005 0.395 -0.218  0.567  1.348  7517 1.000
alpha[3]  -0.099   0.002 0.165 -0.426 -0.099  0.221  5493 1.000
alpha[4]  -0.687   0.001 0.083 -0.855 -0.686 -0.523  7361 1.000
alpha[5]   0.001   0.001 0.122 -0.237  0.001  0.241  6665 0.999
alpha[6]   0.330   0.000 0.050  0.233  0.330  0.426 10574 0.999
alpha[7]   0.340   0.001 0.086  0.175  0.340  0.506  7469 0.999
alpha[8]  -0.777   0.001 0.061 -0.897 -0.776 -0.656  7542 0.999
alpha[9]   0.216   0.001 0.071  0.073  0.216  0.355  7027 1.000
alpha[10] -1.331   0.001 0.098 -1.524 -1.330 -1.136  8231 0.999
alpha[11] -0.406   0.002 0.151 -0.705 -0.406 -0.100  5802 0.999
alpha[12] -0.320   0.001 0.085 -0.488 -0.321 -0.153  7145 1.000
alpha[13] -0.440   0.000 0.041 -0.519 -0.442 -0.361  7392 1.000
alpha[14]  1.369   0.001 0.096  1.177  1.369  1.559  7084 0.999
alpha[15]  0.315   0.002 0.199 -0.083  0.315  0.704  7174 1.000
alpha[16]  1.412   0.001 0.070  1.274  1.412  1.548  6393 0.999
alpha[17]  0.100   0.001 0.071 -0.039  0.099  0.244  7724 0.999
alpha[18] -0.684   0.001 0.057 -0.797 -0.683 -0.574  8749 1.000
alpha[19] -0.596   0.001 0.069 -0.730 -0.596 -0.461  6336 0.999
alpha[20]  0.121   0.001 0.079 -0.036  0.122  0.282  7308 1.000
alpha[21]  0.869   0.001 0.067  0.738  0.869  1.002  6553 1.000
alpha[22]  1.422   0.001 0.122  1.181  1.421  1.667  7990 1.000
alpha[23] -0.357   0.001 0.121 -0.586 -0.357 -0.122  7743 0.999
alpha[24]  0.502   0.001 0.099  0.311  0.501  0.692  7553 0.999
alpha[25]  0.517   0.002 0.181  0.166  0.516  0.881  8580 0.999
beta       0.348   0.000 0.021  0.307  0.348  0.389  3651 1.000
sigma      0.607   0.000 0.011  0.585  0.607  0.630  8275 1.000

Samples were drawn using NUTS(diag_e) at Thu Nov 12 11:58:44 2020.
For each parameter, n_eff is a crude measure of effective sample size,
and Rhat is the potential scale reduction factor on split chains (at 
convergence, Rhat=1).

7) Posterior predictive check to evaluate model fit

# Select 300 samples to plot against observed distribution
color_scheme_set(scheme = "blue")
yrep <- extract(fit_npm)[["y_hat"]]
samples <- sample(nrow(yrep), 300)
ppc_dens_overlay(as.vector(df$log_sales_price_z), yrep[samples, ])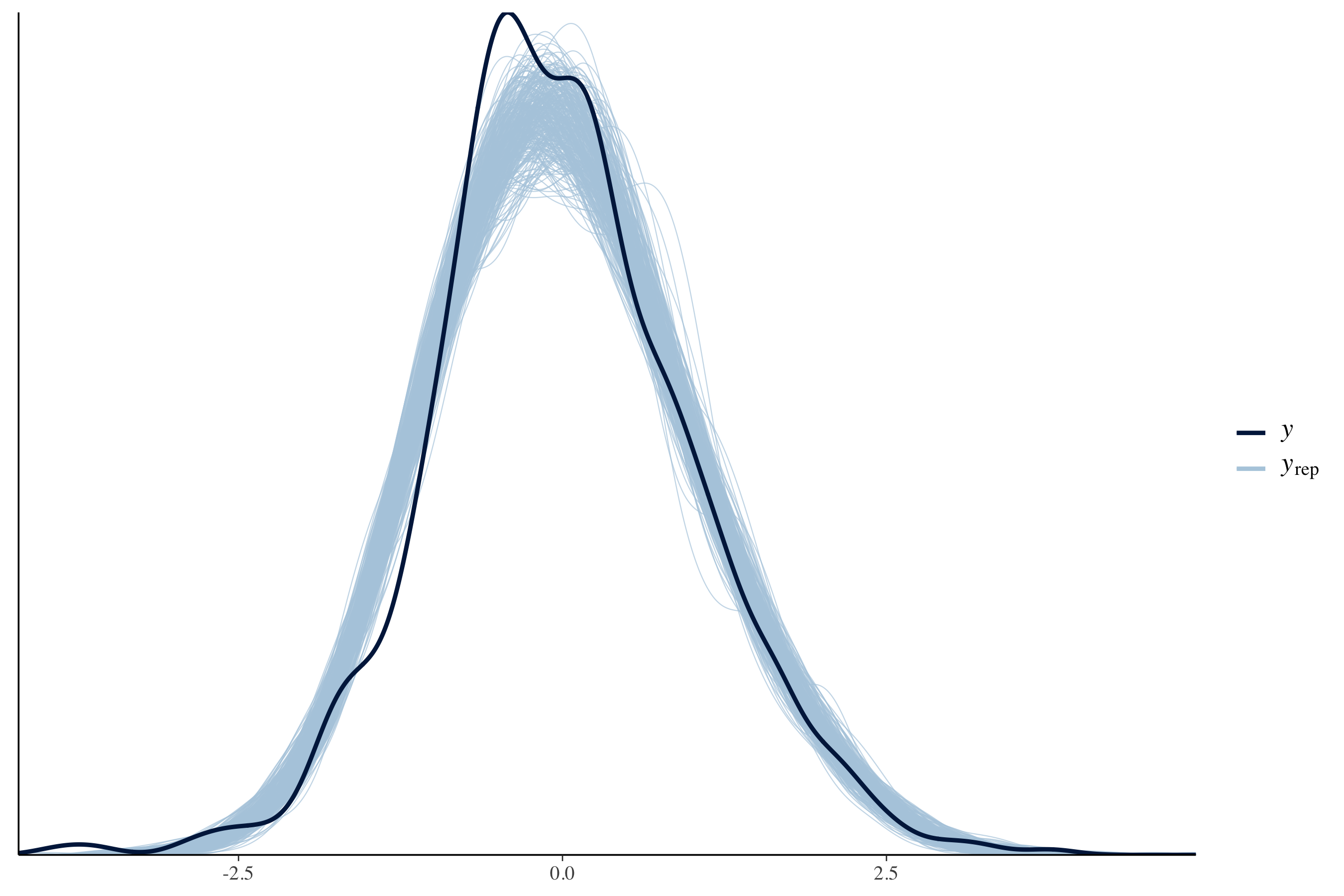

Reversing the data transformations gives back the posterior predictive checks on the natural scale (rescale \(y\) and exponentiate log(SalesPrice) to get back SalesPrice):

# Take 300 samples of posterior predictive checks and revert back to natural scale
ppc <- yrep[samples, ] %>% 
  t() %>% 
  apply(., MARGIN  = 2, FUN = function(x) exp((x * sd(df$log_sales_price)) + mean(df$log_sales_price))) %>% 
  as.data.frame() %>%
  pivot_longer(everything())

# Plot densities
ggplot(ppc, aes(value)) + 
  geom_density(aes(group = name), colour = "lightblue") + 
  geom_density(data = (df %>% select(SalePrice) %>% rename(value = SalePrice)), colour = 'black') +
  theme(legend.position="none", axis.text.y=element_blank()) +
  labs(title = 'Posterior predictive checks - Black: observed SalePrice\nLight Blue: Posterior Samples') +
  ggsave('figures/9r_posterior_predictive_check_outcomescale.png', dpi = 300, height = 6, width = 9)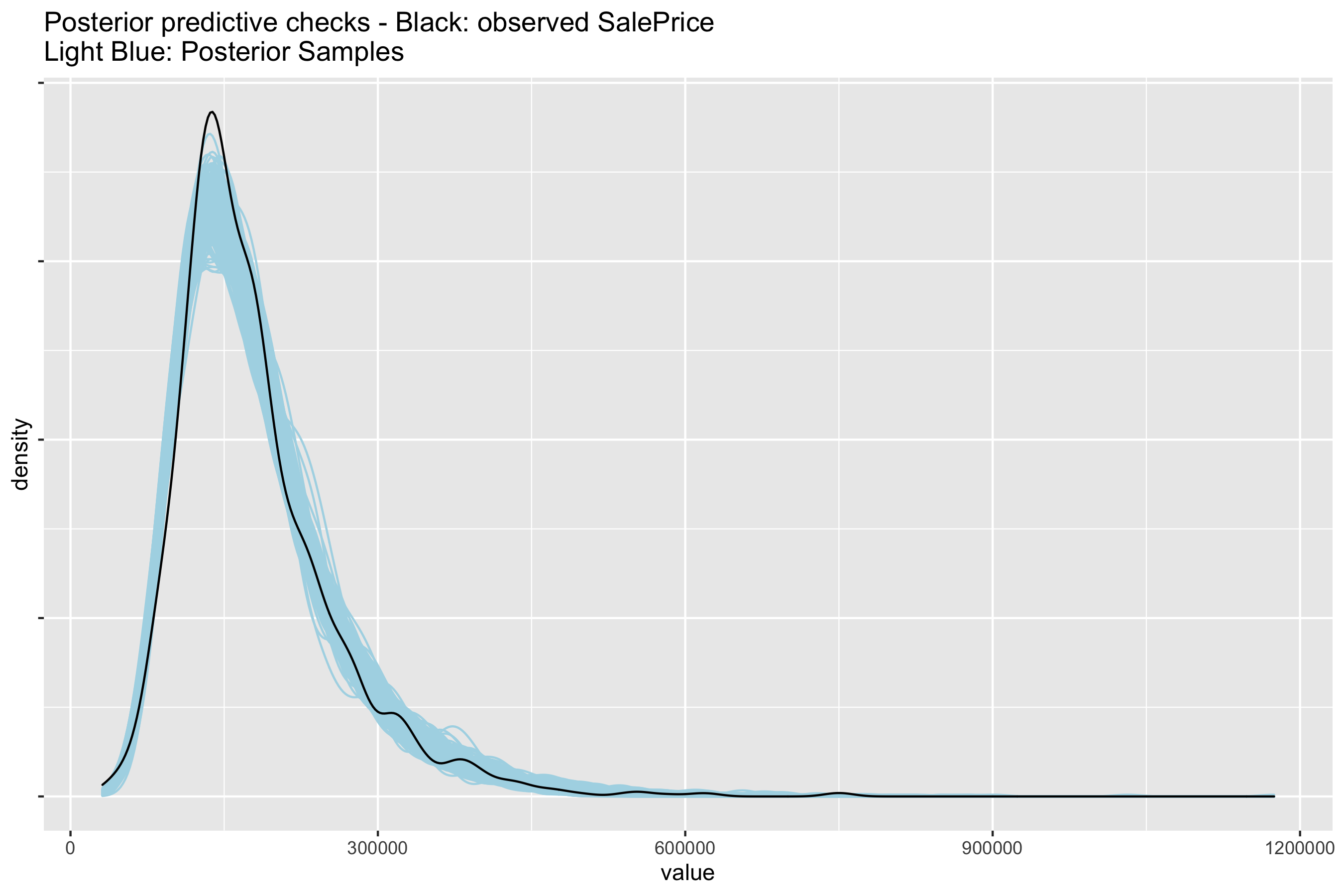

Not bad for a simple model. There is definitely room for iteration and improvement.

Conclusion

The last thing we should do is compare the fits of multiple models and evaluate their performance using cross validation for model selection. The next post applies the full workflow using multilevel models and compares performance using techniques such as Leave One Out - Cross Validation (LOO-CV). Model performance can also be evaluated on out of sample test data as well since this is a predictive task (Kaggle computes the log RMSE of the out of sample dataset).

This is not an exhaustive review of all the diagnostics and visualisations that can be performed in a workflow. There are many ways of evaluating model fit and diagnostics that could validate or invalidate the model. Below are a list of resources which give more detailed examples on various bayesian models and workflows:

Stan case studies
PyMC3 examples
Michael Betancourt’s case study on a Principled Bayesian Workflow and all his other case studies
Bayesian Workflow and some links to the development of bayesian workflow over the past few years can be found here
Robust Statistical Workflow with PyStan
Robust Statistical Workflow with RStan

Notebooks that reproduce the models/plots/etc:

Python

Return home

Original Computing Environment

%load_ext watermark
%watermark -n -v -u -iv -w -a Benjamin_Wee

seaborn 0.11.0
pandas  1.1.3
arviz   0.10.0
pystan  2.19.0.0
numpy   1.19.1
Benjamin_Wee 
last updated: Thu Nov 19 2020 

CPython 3.6.12
IPython 5.8.0
watermark 2.0.2

sessionInfo()

R version 4.0.3 (2020-10-10)
Platform: x86_64-apple-darwin17.0 (64-bit)
Running under: macOS Mojave 10.14.6

Matrix products: default
BLAS:   /System/Library/Frameworks/Accelerate.framework/Versions/A/Frameworks/vecLib.framework/Versions/A/libBLAS.dylib
LAPACK: /Library/Frameworks/R.framework/Versions/4.0/Resources/lib/libRlapack.dylib

Random number generation:
 RNG:     Mersenne-Twister 
 Normal:  Inversion 
 Sample:  Rounding 
 
locale:
[1] en_AU.UTF-8/en_AU.UTF-8/en_AU.UTF-8/C/en_AU.UTF-8/en_AU.UTF-8

attached base packages:
[1] stats     graphics  grDevices utils     datasets  methods   base     

other attached packages:
 [1] gridExtra_2.3        gdtools_0.2.2        svglite_1.2.3.2      bayesplot_1.7.2      rstan_2.21.2        
 [6] StanHeaders_2.21.0-6 forcats_0.5.0        stringr_1.4.0        dplyr_1.0.2          purrr_0.3.4         
[11] readr_1.4.0          tidyr_1.1.2          tibble_3.0.4         ggplot2_3.3.2        tidyverse_1.3.0     

loaded via a namespace (and not attached):
 [1] httr_1.4.2         jsonlite_1.7.1     splines_4.0.3      modelr_0.1.8       RcppParallel_5.0.2 assertthat_0.2.1  
 [7] stats4_4.0.3       cellranger_1.1.0   yaml_2.2.1         pillar_1.4.6       backports_1.2.0    lattice_0.20-41   
[13] reticulate_1.18    glue_1.4.2         digest_0.6.27      rvest_0.3.6        colorspace_1.4-1   htmltools_0.5.0   
[19] Matrix_1.2-18      plyr_1.8.6         pkgconfig_2.0.3    broom_0.7.2        haven_2.3.1        scales_1.1.1      
[25] processx_3.4.4     mgcv_1.8-33        generics_0.1.0     farver_2.0.3       ellipsis_0.3.1     withr_2.3.0       
[31] cli_2.1.0          magrittr_1.5       crayon_1.3.4       readxl_1.3.1       evaluate_0.14      ps_1.4.0          
[37] fs_1.5.0           fansi_0.4.1        nlme_3.1-149       xml2_1.3.2         pkgbuild_1.1.0     tools_4.0.3       
[43] loo_2.3.1          prettyunits_1.1.1  hms_0.5.3          lifecycle_0.2.0    matrixStats_0.57.0 V8_3.4.0          
[49] munsell_0.5.0      reprex_0.3.0       callr_3.5.1        compiler_4.0.3     systemfonts_0.3.2  rlang_0.4.8       
[55] grid_4.0.3         ggridges_0.5.2     rstudioapi_0.11    labeling_0.4.2     rmarkdown_2.5      gtable_0.3.0      
[61] codetools_0.2-16   inline_0.3.16      DBI_1.1.0          curl_4.3           reshape2_1.4.4     R6_2.5.0          
[67] lubridate_1.7.9    knitr_1.30         utf8_1.1.4         stringi_1.5.3      parallel_4.0.3     Rcpp_1.0.5        
[73] vctrs_0.3.4        dbplyr_2.0.0       tidyselect_1.1.0   xfun_0.19